Exam 1 Results
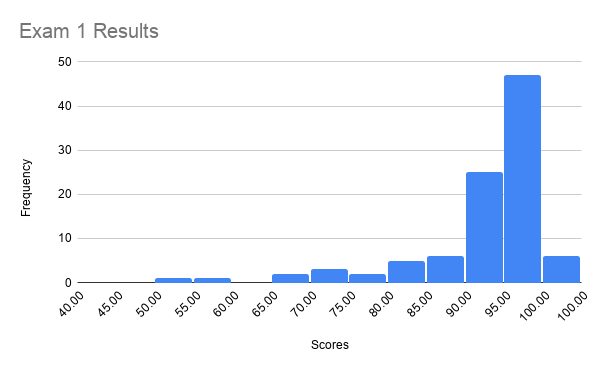
| Mean | 90.5 |
| Median | 95.0 |
| Mode | 94.6 |
| Standard Deviation | 15.8 |
| Range | 100.0 |
| Minimum | 0.0 |
| Maximum | 100.0 |
| Sum | 9047.7 |
| Count | 100.0 |
Category: f19-busad265
| Mean | 90.5 |
| Median | 95.0 |
| Mode | 94.6 |
| Standard Deviation | 15.8 |
| Range | 100.0 |
| Minimum | 0.0 |
| Maximum | 100.0 |
| Sum | 9047.7 |
| Count | 100.0 |

Review:
Presentation:
Activity:
Assignment:
Review:
Presentation:
Solving Normal Curve Problems
Activity:
Study:
Review:
Presentation:
Activity:
Problem 1. The distribution of heights of young women (18 – 24 years old) is approximately normal with mean = 64.5 inches and standard deviation = 2.5 inches.
Problem 2. There are two national college-entrance examinations, the SAT and the ACT. Scores on individual SAT exams are approximately normal with mean = 500 and standard deviation=100. Scores on the ACT exams are approximately normal with mean = 18 and standard deviation = 6.
Problem 3. Find the percentage of observations from a standard normal distribution that satisfy the following. Also, draw a normal curve and shade the corresponding area under the curve.
Assignment:
Review:
Presentation:
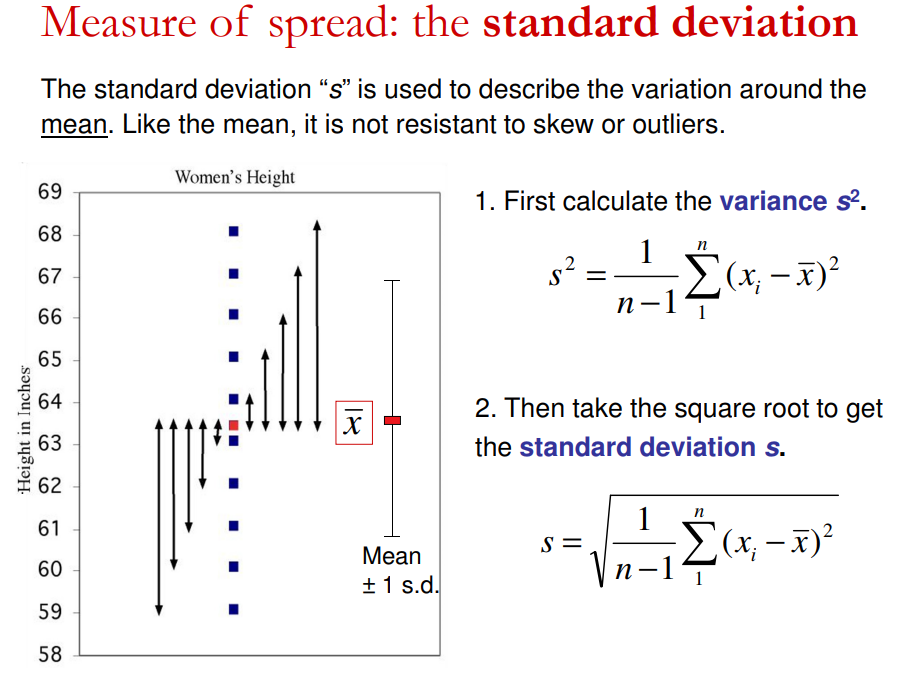
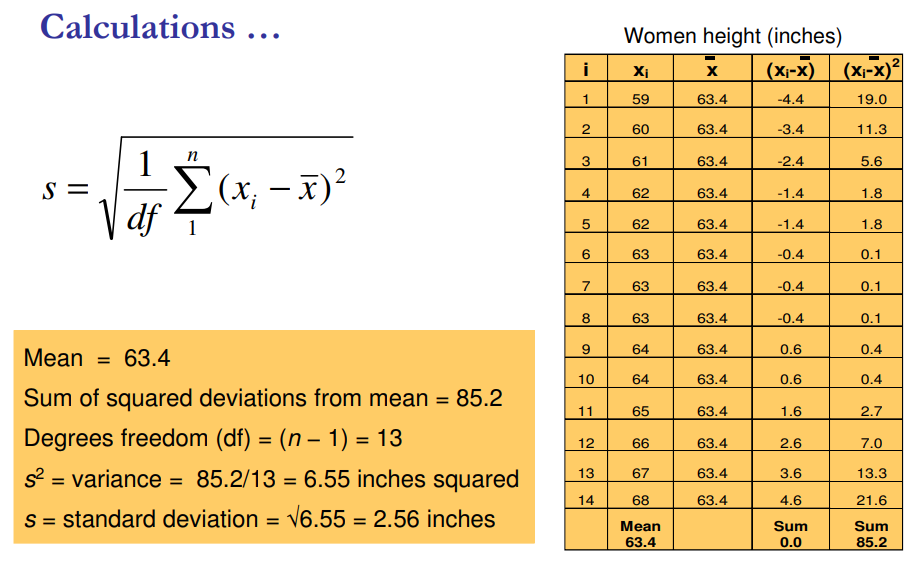
Activity:
Problem 1. Below are the number of home runs that Babe Ruth hit in each of his 15 years with the New York Yankees, 1920 – 1934. Calculate the mean and standard deviation.
54 59 35 41 46 25 47 60 54 46 49 46 41 34 22
Problem 2. Six 9th-grade students and six 12th-grade students were asked: how many movies have you seen this month? See their responses below. Calculate the mean and standard deviation for each data set. Which is more spread out, the 9th-grade or 12th-grade data?
9th-grade: 5, 1, 2, 5, 3, 8
12th-grade: 4, 2, 0, 2, 3, 1
Assignment:
Review:
Presentation:
Activity:
Problem 1.
Here are the starting salaries, in thousands of dollars, offered to 20 students who earned bachelor’s degrees in computer science in 2011.
63 56 66 77 50 53 78 55 90 65 64 69 59 76 48 54 49 68 51 50
a. Make a stemplot.
b. Find the median, mean and mode.
c. Find the five-number summary.
d. Make a boxplot.
e. Compute the range and interquartile range (IQR).
Problem 2.
A consumer testing lab measured calories per hot dog in 20 brands of beef hot dogs. Here are the results:
186 181 176 149 184 190 158 139 175 148 152 111 141 153 190 157 131 149 135 132
a. Make a stemplot.
b. Find the median, mean and mode.
c. Find the five-number summary.
d. Make a boxplot.
e. Compute the range and interquartile range (IQR).
These problem descriptions (#1 and #2) are from “Against All Odds”, modified slightly and copied here for convenience.
Problem 3.
Use the MPG data for top selling midsize cars in the US and European markets from Lesson 1.
a. Find the five-number summaries.
b. Produce 2 boxplots, one for each market, and put them both on the same axes to facilitate comparison.
Assignment:
Review:
Presentation:
Activity:
Study:
Activity Data:
Top Selling Midsize Cars in the US – MPG
Top Selling Midsize Cars in the Europe – MPG
Presentation:
Activity:
Study: