Exam 2 Results
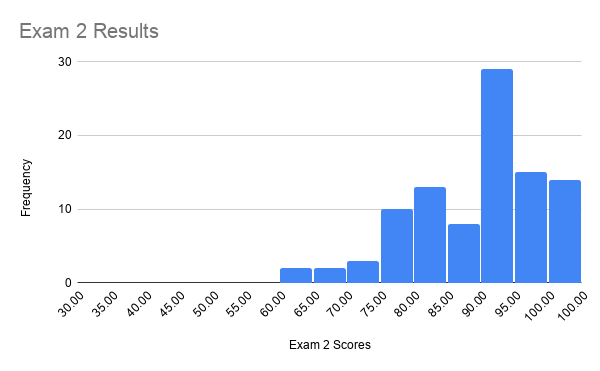
| Exam 2 | |
| Mean | 85.4 |
| Median | 90.8 |
| Standard Deviation | 19.8 |
| Range | 100.0 |
| Minimum | 0.0 |
| Maximum | 100.0 |
| Sum | 8535.1 |
| Count | 100.0 |
Category: f19-busad265
| Exam 2 | |
| Mean | 85.4 |
| Median | 90.8 |
| Standard Deviation | 19.8 |
| Range | 100.0 |
| Minimum | 0.0 |
| Maximum | 100.0 |
| Sum | 8535.1 |
| Count | 100.0 |

Review:
Exam 2 Topics:
Activity:
Review:
Presentation:
Review:
Presentation:

Activity:
Determine whether it’s a 1-sided or 2-sided hypothesis test and solve. Report p-values and determine if you can reject or must fail to reject the null hypothesis.
Review:
Presentation:
Assignment:
* Most example and activity problems presented above are derived from Moore, D.S., McCabe, G.P., and Craig, B.A., 2009. Introduction to the Practice of Statistics, 6th Edition. New York: W.H. Freeman and Company.
Review:
Presentation:
Activity:
Review:
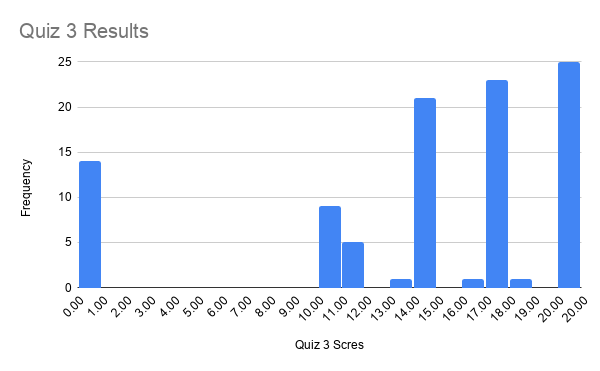
Presentation:
Activity:
These examples and problems are from the Against All Odds video series and Introduction to the Practice of Statistics (6th Ed.) by Moore et al.
Review:
Presentation:
Activity:
Assignment:
Review:
Presentation:
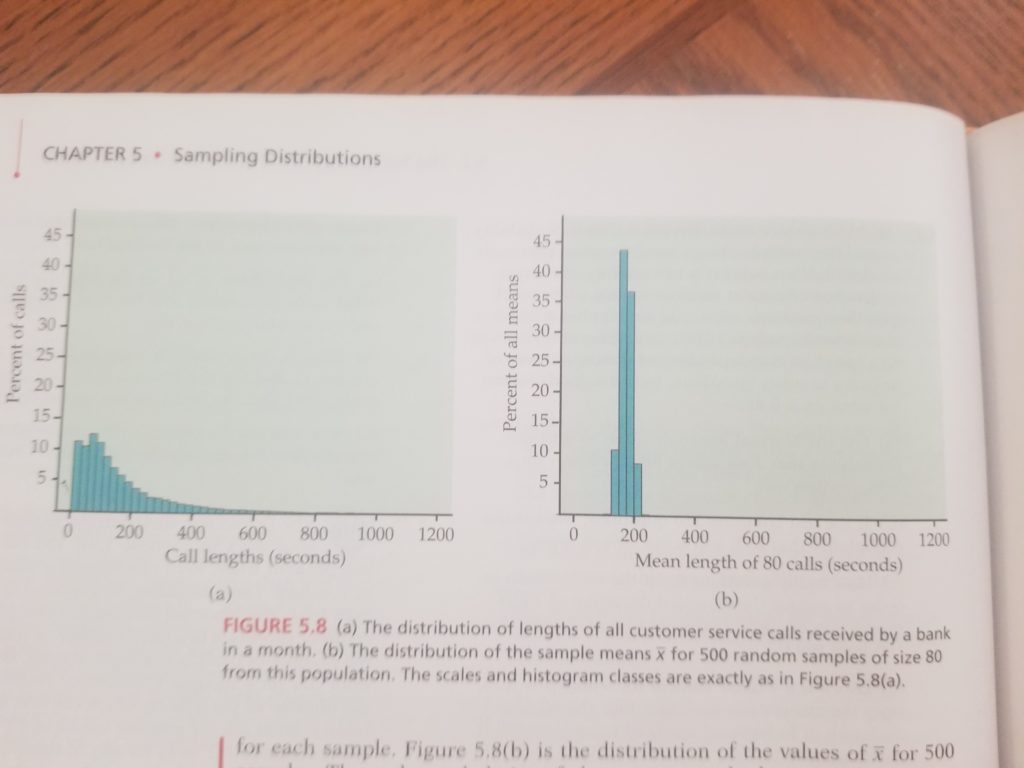
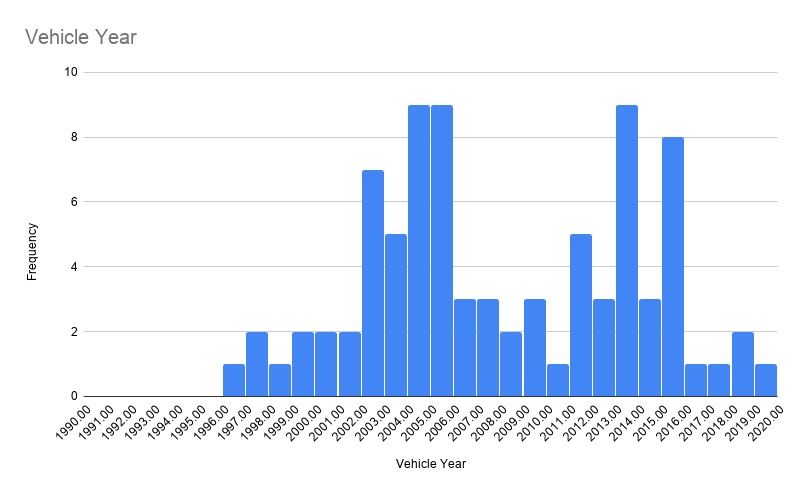
Activity:
Study:
| Mean | 2007.65 |
| Standard Error | 0.63 |
| Median | 2006.50 |
| Mode | 2013.00 |
| Standard Deviation | 5.77 |
| Range | 23.00 |
| Minimum | 1996.00 |
| Maximum | 2019.00 |
| Sum | 168643.00 |
| Count | 84.00 |
| Largest(1) | 2019.00 |
| Smallest(1) | 1996.00 |
| sampling distribution mean | 2007.65 |
| sampling distribution stdev | 0.63 |
Review:
Presentation:
Activity:
Assignment: