Category: f18-busad265

Final Exam Results

I’ve graded all Final Exams. Here are the results. Please email me if you want your final exam score and final grade.

Thanks for a great semester! Enjoy your break!

x̅ = 86.1, s=11.0

More

Review for Final Exam, Part 2

Review:

  • Review for Final Exam, Part 1
  • Student evaluations
  • Final Exam Schedule
    • MW 11:15 Section: Mon @ 10:30 am in HSB 108
    • MW 1:00 Section: Mon @ 1:00 pm in HSB 110

Review:

  • Sampling
    • Census vs Sampling
    • Sampling Types
      • Voluntary response
      • Simple random sample (SRS)
      • Stratified random sample
    • Sampling Distributions
    • Central Limit Theorem
  • Estimation with Confidence Intervals
  • t-distribution for small samples (bring a t-table!)
  • Inference for Proportions
  • Significance Testing

Activity:

Study:

  • Vocabulary words you should know/understand
    • distribution, shape, skew, stemplot, histogram
    • percentile, quartile, IQR
    • spread (of data), mean, standard variation, variance
    • normal distribution, normal curve, standard normal, Z-Score
    • scatterplot, dependent vs independent variable, explanatory vs response variable
    • positive vs negative correlation, strong/moderate/weak correlation
    • regression, linear equation, pearson correlation coefficient, r-squared
    • outliers, spurious correlation, retrospective study, prospective study
    • sample, bias, treatment
    • sampling distribution, central limit theorem
    • confidence level/interval, margin of error
    • inference, proportions, t-table
    • null hypothesis, alternative hypothesis, significance level
    • one-tail test, two-tail test
More

Review for Final Exam, Part 1

Review:

  • Exam 3 Results
  • Student Evaluations and final exam
  • Spring Courses
    • BUSAD 360 Advanced Statistics (MW 11:15 and 1:00)
    • ECON 320 Geography of World Economy (TTh 11:15)

Final Exam:

  • Comprehensive
  • Venue: HSB 110
  • Exam day/times:
    • Sec 1: Mon @ 10:30 am
    • Sec 2: Mon @ 1:00 pm

Review Topics:

  •  Distributions
    • Stemplots
    • Histograms
  • Measures of Center
    • Mean
    • Median
    • Percentiles
  • Boxplots
    • Quartiles
    • 5-number summary
  • Measuring the “spread” of the data
    • Variance
    • Standard Deviation
  • Normal Curves
    • Standard Normal
    • Z-Scores
    • Z-table (bring a print out!)
    • Solving normal curve problems
      • less than
      • greater than
      • between
      • reverse look up (solve for x rather than Z)
  • Scatterplots
  • Linear Regression
    • Sum of Squares
    • Regression line calculations
    • Pearson Correlation Coefficient
    • R-Squared

Activity:

More

Exam 3 Results

Exam 3
Mean 83.5
Standard Error 1.3
Median 84.4
Mode 93.8
Standard Deviation 10.2
Sample Variance 104.6
Kurtosis 0.5
Skewness -0.7
Range 45.0
Minimum 55.0
Maximum 100.0
Sum 5430.7
Count 66.0

 

More

Review for Exam 3

Exam on Wed, Nov 14

Exam 3 Topics:

  • Sampling Distributions
  • Central Limit Theorem
  • Estimation
    • Confidence Intervals = Point estimate +/- Margin of error
    • t-distribution for small samples
    • Inference for Proportions
  • Significance Testing
    • Step 1. Set up Ho and Ha
    • Step 2. Calculate Z statistic
    • Step 3. Calculate p-value
    • Step 4. Compare p-value to alpha (0.05) and decide to Reject Ho or Fail to Reject Ho
    • 1-tail vs 2-tail hypothesis testing

Assignment:

More

Lesson 19: One-Tail vs Two-Tail Significance Testing

Review:

Presentation:

  • Hypothesis testing: 1-tail vs 2-tail
  • 2-Tail Tests
    • Example 6.15 (p. 383-384):
      • Ho: μ = 168, Ha: μ ≠ 168, x-bar = 173.7, n=71, σ = 27, α = 0.05
    • Use Your Knowledge 6.43 (p. 385-386):
      • Ho: μ = 25, Ha: μ ≠ 25, x-bar = 27, n=25, σ = 5, α = 0.05
  • Compare >, < and ≠
    • Z = -1.73
    • What is the p-value for
      • Ha: μ > μo [use 1 – P(Z)]
      • Ha: μ < μo [use P(Z)]
      • Ha: μ ≠ μo [multiply by 2]

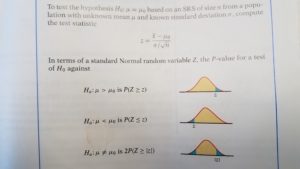
Activity:

Determine whether it’s a 1-sided or 2-sided hypothesis test and solve. Report p-values and determine if you can reject or must fail to reject the null hypothesis.

  1. A test of the null hypothesis Ho: μ = μo yields test statistic z = 1.34.
    1. What is the P-value if the alternative is Ha: μ > μo
    2. What is the P-value if the alternative is Ha: μ < μo
    3. What is the P-value if the alternative is Ha: μ ≠ μo
  2. The college bookstore tells students the average textbook price is $52 with a standard deviation of $4.50. A group of students thinks the average price is higher. In order to test the bookstore’s claim, the students select a random sample of size 100 and find a sample mean price of $52.80. Perform a hypothesis test to determine if the price difference is significantly higher for α = 0.05.
  3. A certain chemical pollutant in the Arkansas River has been constant for several years with mean μ = 34 ppm (parts per million) and standard deviation σ = 8 ppm. A group of factory representatives whose companies discharge liquids into the river is now claiming they have lowered the average with improved filtration devices. A group of environmentalists will test to see if this is true. Assume their sample of size 50 gives a mean of 32.5 ppm. Perform a hypothesis test to determine if the pollution levels are significantly lower for α = 0.05.
  4. A manufacturing process produces ball bearings with diameters that have a normal distribution with mean, μ = 0.50 centimeters and known standard deviation, σ = .04 centimeters. Ball bearings with diameters that are too small or too large are problematic.
    1. Assume a random sample n=25 with a sample mean diameter = 0.51 cm. Perform a hypothesis test at α = 0.05.
    2. Assume a random sample n=25 with a sample mean diameter = 0.48 cm. Perform a hypothesis test at α = 0.05.
More

Lesson 18: Tests of Significance

Review:

  • Estimation with Confidence Intervals
  • Small Sample Estimation
  • Inference for Proportions
  • Polling
  • Exam 3 on Wed, Nov 14

Presentation:

  • Significance Testing
    • aka Hypothesis Testing
    • Purpose: to evaluate data for evidence of significant agreement or disagreement
  • Significance testing is like paternity testing.
    • When you check father-child DNA for a match you can prove one person is or is not the father.
    • The same test does not prove another person is the father.
    • You’re evaluating only one possibility at a time.
  • Significance Testing video
  • Step 1. Setup the null hypothesis (Ho) and alternate hypothesis (Ha)
  • Step 2. Calculate the appropriate test statistic
  • Step 3. Find the P-value (probability of obtaining result by chance)
  • Step 4. Interpret results, compare P-value to α = 0.05 ; if P-value < 0.05, “Reject Ho” else “Fail to Reject Ho”
  • Example A: Do Math SAT scores improve significantly with coaching?
    • National Math SAT scores are normally distributed with mean score = 505 and std. dev = 62
    • Sampled 1,000 students who received coaching
    • Sample mean score was 509
    • Are these results significantly better than the national average?
    • Step 1: Setup the hypothesis test

    μ = 505, σ = 62
    x̅ = 509, n = 1,000
    Ho: μ = 505
    Ha: μ > 505

    • Step 2: Calculate the appropriate test statistic
      • Z-test = (x̅ – μ)/(σ/√n)
      • (509 – 505)/(62/√1000) = 4/1.96 = 2.04
    • Step 3: Find P-value
      • P = 1 – P(Z<2.04) = 1 – 0.9793 = 0.0207
    • Step 4: Interpret results
      • 0.0207 ≅ 2.07% probability of getting this result by chance
      • 0.0207 < 0.05
      • Reject Ho
      • Coaching seems to improve scores significantly
  • Example B: Has a student paper been plagiarized?
    • Previous student papers contain 7 unique vocabulary words on average with std dev of 2.6
    • Submitted paper contains 10 unique words
    • Is the submitted paper significantly different?
    • Step 1: Setup the hypothesis test
      • μ = 7, σ = 2.6
        x̅ = 10
        Ho: μ = 7
        Ha: μ > 7
    • Step 2: Calculate the appropriate test statistic
      • Z-test = (x̅ – μ)/(σ/√n)
      • (10 – 7)/2.6 = 1.15
    • Step 3: Find P-value
      • P = 1 – P(Z<1.15) = 1 – 0.8749 = 0.1251
    • Step 4: Interpret results
      • 0.1251 ≅ 12.51% probability of getting result by chance
      • 0.1251 > 0.05
      • Fail to Reject Ho
      • Unique vocabulary is within normal range, no evidence of plagiarism

Assignment:

  • Problem 1.1. More than 200,000 people worldwide take the GMAT examination each year as they apply for MBA programs. Their scores vary Normally with mean about μ = 525 and standard deviation about σ = 100. One hundred students, n = 100, go through a rigorous training program designed to raise their GMAT scores. The students who go through the program have an average score of x̅ = 541.4. Is there evidence to suggest the training program significantly improves GMAT scores?
  • Problem 1.2. A newly installed rooftop solar system has been producing energy for n = 100 days. Average energy production is 41.8 kWh per day with a standard deviation of 13.9 kWh. The solar panel manufacturer claims the panels typically produce 40 kWh per day. Is the newly installed system producing significantly more energy than estimated by the manufacturer?

* Most example and activity problems presented above are derived from Moore, D.S., McCabe, G.P., and Craig, B.A., 2009. Introduction to the Practice of Statistics, 6th Edition. New York: W.H. Freeman and Company. 

More

Lesson 17: Political Polling in Colorado Congressional District 3

Voter Polling Assignment:

Follow this link and find your name (listed alphabetically): Voter Polling

Rules:

  1. Be polite!
  2. Keep the call brief and to the point.
  3. Introduce yourself as a student at Colorado State University – Pueblo, working on a class assignment.
  4. Ask if they plan to vote in next week’s election. Some may have already voted by mail. [Record Yes or No in the worksheet]
  5. Ask who they support for US House of Representatives: Scott Tipton (Republican) or Diane Mitsch Bush (Democrat) [Record “Tipton”, “Bush” or “Other” according to their preference].
  6. Thank them for taking the time to answer.
  7. If someone becomes belligerent, apologize for disturbing them and end the call.
  8. If someone demands to know why they were contacted, you can provide my name and office phone: 719-549-2684.
  9. Please don’t fabricate voter responses. If you can’t stomach making the phone calls then just don’t do it. Fake data will poison our survey. If I suspect you “invented” the responses I will ask for calling records.
  10. If they feel like talking, listen and take notes. This anecdotal information might be more valuable than the simple yes/no and candidate preference data.

Here’s a simple script you can use:

  • “Hello, this is Justin. I’m a student calling from Colorado State University – Pueblo, working on a class assignment. Do you plan to vote in the election next week?”
  • Record response.
  • “Who do you support in the race for US House of Representatives, Republican Scott Tipton or Democrat Diane Mitsch Bush?”
  • Record response.
  • “That’s it. Thank you for your time!”

 

More

Lesson 16: Inference for Proportions

Review:

  • t-distribution for small samples
  • class on Thu

Presentation:

  • How to Estimate a Population Proportion
    • Conduct a Simple Random Sample (SRS) of size n
    • Record the count, x, of “successes”, e.g., # of voters supporting candidate A
    • Calculate the sample proportion, p-hat = x/n
    • If n is sufficiently large (≥30), we can assume p-hat is Normally distributed
    • Estimate of the population proportion mean, μ = p-hat
    • Estimate of the population proportion std dev, σ = √(p*(1-p)/n)
    • Estimate margin of error, m = z*σ  (use z = 1.96 for 95% confidence)
    • Estimate with 95% confidence interval is p-hat ± m
    • Same procedure for a small sample size (<30) using the t distribution and substituting t* for z*
  • Example 8.1 on p. 489 – Binge Drinking Survey
    • n = 13,819
    • x = 3,140
    • p-hat = 3140/13819 = 0.227
    • standard deviation = √(p-hat*(1-p-hat)/n) = 0.00356
    • p-hat ± z*√(p-hat*(1-p-hat)/n) = 0.227 ± 1.96*(0.00356) = 0.227 ± 0.007
    • {0.220,0.234}

Activity:

  1. A random sample of 2,454 12th-grade students were asked the following question: Taking all things together, how would you say things are these days – would you say you’re happy or not too happy? Of the responses, 2,098 students selected happy. Determine the sample proportion of students who responded they were happy and calculate a 95% confidence interval for the population proportion of 12th-grade students who are happy.
  2. Currently, mothers in North America are advised to put babies to sleep on their backs. This recommendation has reduced the number of cases of sudden infant death syndrome (SIDS). However, it is a likely cause of another problem, i.e., flat spots on babies’ heads. A study of 440 babies aged 7 – 12 weeks found that 46.6% had flat spots on their heads. Calculate a 95% confidence interval for the proportion of babies in this age group that have flat spots.
  3. A phone survey contacted 1,910 households in which a computer was owned and respondents were asked if they could access the Internet from their home. A total of 1,816 of the households responded yes. Calculate a 95% confidence interval to estimate the proportion of American households with internet access.

Assignment:

You will be assigned a number of registered voters in Congressional District 3. You will telephone each voter on the list and ask two questions. First, introduce yourself as a CSU-Pueblo student working on an assignment for your statistics class. Then, ask these two questions:

  1. Do you plan to vote in next week’s election?
  2. Who do you support in the race for US House of Representatives: Republican Scott Tipton or Democrat Diane Mitsch Bush?

Ask both questions, even if the answer to #1 is “no”. Once all surveys have been completed and response data compiled you will use the data to estimate vote percentages for both candidates in your assigned county.

More

Lesson 15: The t-distribution for Small Sample Inference

Review:

  • Estimation with Confidence Intervals

Presentation:

  • t-distribution
    • For larger samples, n ≥ 30 use Z-table
    • For small samples, n < 30 use t-distribution
    • Only impacts calculation of the test statistic
      • margin of error for confidence intervals
      • test statistic and p-value for significance testing (don’t worry, we’ll cover  these topics later)
    • t distribution critical values
      • print the t distribution table for the next exam
        • use the “0.025” column for estimation with 95% confidence intervals
      • select the row corresponding to df = n – 1
        • df = degrees of freedom
        • n = number of records in sample data
      • find the t* critical value
        • row = df = n – 1
        • column = .025 (top label) or 95% confidence level (bottom label)
        • e.g., if n = 13
          • df = n – 1 = 12
          • go to the row where df = 12 and move to the .025 column
          • you should find t* = 2.179
    • t-statistic formulas
      • for confidence intervals
        • x-bar ± t * s/√n
        • instead of the Z equivalent:  x-bar ± z * σ/√n
    • Video
    • Examples:
      • Identify appropriate t distribution critical values
        • n=10 with 95% confidence, t* = 2.262
        • n=20 with 95% confidence, t* = 2.093
      • A sample of size n = 20 produced the sample mean, x-bar = 36.0 and standard deviation, s = 9.0. Construct a 95% confidence interval to estimate the population mean.
        • n = 25, x-bar = 36.0, s = 9.0
        • df = 24, t* = 2.064
        • m = 2.064*(9/(√25)) = 3.7152
        • Estimate for μ = 36.0 ± 3.7152
        • 95% confidence interval: [32.2848, 39.7152]
          • previous lesson interval with Z=1.96 and n=400: [35.118, 36.882]
          • sample size can make a big difference

Activity:

  • Problem 1. Use the t distribution table, assuming 95% confidence, to find the value of t* for each of the following sample sizes.
    • n = 12
    • n = 18
    • n = 24
    • n = 30
  • Problem 2. The weights (in lbs) from a random sample of n=16 four-year-old children who took part in a study on childhood obesity are provided below. Estimate the mean weight of four-year-old children using a 95% confidence interval.
    • {37.1, 26.7, 36.1, 36.2, 40.3, 43.9, 36.2, 40.7, 42.5, 34.8, 37.9, 34.5, 31.1, 36.4, 35.7, 33.4}
  • Problem 3. After purchasing a new fuel-efficient vehicle, the owner calculates miles per gallon (mpg) the first n=12 times he fills the fuel tank. His calculations are provided below. Estimate vehicle fuel efficiency using a 95% confidence interval.
    • {42, 43, 37, 36, 34, 45, 48, 43, 38, 42, 43, 46}

These examples and problems are from the Against All Odds video series and Introduction to the Practice of Statistics (6th Ed.) by Moore et al.

Assignment:

More