Lesson 11: Random Variables
October 4, 2017
Review:
- Probability
- Exam 2 on Wed, Oct 11
Presentation:
- Random Variables
- Discrete Random Variables
- Probability distribution table
- Continuous Random Variables
- Area under a density curve
- video
- Discrete Random Variables
- Example Problem
- The random variable x, defined below, gives the average grade of 12th grade students in U.S. high schools. The probability distribution for x is given in Table 20.11.
x = {4 if A average, 3 if B average, 2 if C average, 1 if D average}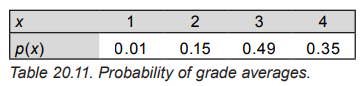
a. Find P x( 3) ≥ , the probability that a randomly selected student has a B or better average.
b. Find P x( 3) < , the probability that a randomly selected student has a below B average. How is this probability related to your answer to (a)?
c. Make a probability histogram for the distribution of x. What does your graphic display tell you about the distribution of average grades?
- The random variable x, defined below, gives the average grade of 12th grade students in U.S. high schools. The probability distribution for x is given in Table 20.11.
Assignment:
Problem 1. The U.S. government collects data on many variables having to do with households.
Let x = the number of children under 15 in a household. The probability distribution for x is shown in the table below.

a. What is the probability that a randomly selected household has at least one child under 15?
b. What is the probability that a randomly selected household has between two and four children under 15? In other words, find P (2 ≤ x ≤ 4).
c. Draw a probability histogram that represents the probability distribution shown in the table above.
Problem 2. Assume that the distribution of weight for 7½-week old hens is normally distributed with mean 544 grams and standard deviation 49 grams. Let w = weight of a randomly selected hen.
a. Sketch normal density curve representing the distribution of w.
Use technology or the standard normal table to find the probabilities in (b) – (d). On a copy of the normal density curve that you sketched for (a), shade the area under the curve that represents each probability.
b. P ( w < 500)
c. P (w ≥ 580)
d. P (500 ≤ w ≤ 580)
Problems 1 and 2 are from AgainstAllOdds_StudentGuide_Unit20 duplicated here for convenience.